
 |
Markovian Boolean Stochastic Simulator |  |
MaBoSS ProjectMaBoSS is a C++ software for simulating continuous/discrete time Markov processes, applied on a Boolean network. MaBoSS uses a specific language for associating transition rates to each node. Given some initial conditions, MaBoSS applies Monte-Carlo kinetic algorithm (or Gillespie algorithm) to the network to produce time trajectories. Time evolution of probabilities are estimated. In addition, global and semi-global characterizations of the whole system are computed. A new version is available (2.0): it is an environment made of a core C++ script and a set of tools. In the core script, the initial condition grammar has been extended, probabilities of fixed points are estimated and export in Boolean logic is available. MaBoSS should be intalled in an unix-based OS (Linux, MacOSX). The core C++ script can be also installed on Windows through Cygwin MaBoSS source code is available on GitHub : https://github.com/sysbio-curie/MaBoSS-env-2.0 The standard version of MaBoSS supports up to 64 nodes per network. If you need more nodes per network, you have to add an extra hint to the compilation command (see README on MaBoSS' GitHub). Using AnacondaThe simplest way to install MaBoSS is using Anaconda package available in the CoLoMoTo repository with :conda install -c colomoto maboss Using pre-compiled binariesMultiple versions are provided, depending in the maximum number of nodes you want to simulate.
Installation of full MaBoSS environment
Installation of only MaBoSS core C++This procedure is not necessary if MaBoSS environment (above) is installed.
MaBoSS can be used in windows, through Cygwin (see README file). The old versions of MaBoSS are available here: How to use MaBoSS environment
MaBoSS (and MaBoSS_##n for higher
maximum number of nodes): Reference Card for version 2.0
MBSS_FormatTable.pl: Description
and README.
Compatible with MaBoSS_##n, by specifying the executable name with -mb option.
MBSS_SensitivityAnalysis.pl: Description
and README.
Need to modify produced shell script if excecutable is MaBoSS_##n.
MBSS_DrugSim.py: Description and README.
Need to modify produced shell script if excecutable is MaBoSS_##n.
MBSS_PrepareProjectFile.sh: Description
and README.
A MaBoSS 2.0 tutorial is available, based on an example that illustrates all MaBoSS environment functionalites. For this tutorial, the following files are necessary:Compatible with MaBoSS_##n (excecutable name can be specified in .pmbss file). Model in GINsim format Configuration file for MBSS_DrugSim.py Profile file for MBSS_MultipleSim.py File for MBSS_PrepareProjectFile.sh How to build a mathematical model from scratchIf you wish to build your logical model directly, here are the steps on how to proceed (full environment is not necessary, only core C++ is needed).
Toy ModelModel Description
The toy model presented here is a simple example consisting of three nodes: A, B and C. A can be activated by C and inhibited by B, B is only activated by A and C is activated by both A and B. This example illustrates the case of a simple loop in the transition graph. We propose to study two cases with two different transition rates for one of the transitions: fast and slow.
Influence Graph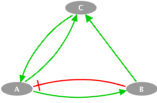
Transition GraphSince the model is small enough, we first chose to run it with asynchronous updating strategy in GINsim to visualize the transition graph. The transition graph shows the fixed point [ABC]=[000]. It also shows a possible cycle: [101]=>[111]=>[011]=>[001]. At [001], the system can either continue to cycle or escape the cycle and go to the steady state [000]. We will explore the dynamics in the case that this "escape" rate is slow or fast. 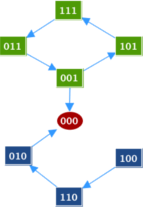
Model
The model can be written as follows:
Node A {
rate_up=(C AND (NOT B)) ? $Au : 0.0;
rate_down= B ? $Ad : 0.0;
}
Node B {
rate_up= A ? $Au : 0.0;
rate_down = A ? 0.0 : $Ad ;
}
Node C{
rate_up=0.0;
rate_down=((NOT A) AND (NOT B)) ? $escape : 0.0 ;
}
In the configuration file, we set the values for the parameters: Au, Bu, Ad, Bd and escape. The parameter "escape" corresponds to the degradation of C. In the fast case, escape=10, and in the slow case, escape=0.00001. Initial values for these simulations are set to 1.
BND and configuration files can be found here:
Command lines: MaBoSS -c Four_cycle_FEscape.cfg -o Four_cycle_FEscape Four_cycle.bnd MaBoSS -c Four_cycle_SEscape.cfg -o Four_cycle_SEscape Four_cycle.bnd MaBoSS -c Four_cycle_SEscape_long.cfg -o Four_cycle_SEscape_long Four_cycle.bnd ResultsThere are several outputs of the simulations. Two of them present a particular interest for the biological interpretation of these simulations. The first one allows to follow the probabilities of each state and the entropy and transition entropy as a function of time (see probtraj files). The second one describes the asymptotic behaviour of the system, i.e. its possible stationary distributions (statdist files). For the case of the fast escape, the probability to reach the stable steady state tends to 1. Both entropy and transition entropy tend to 0 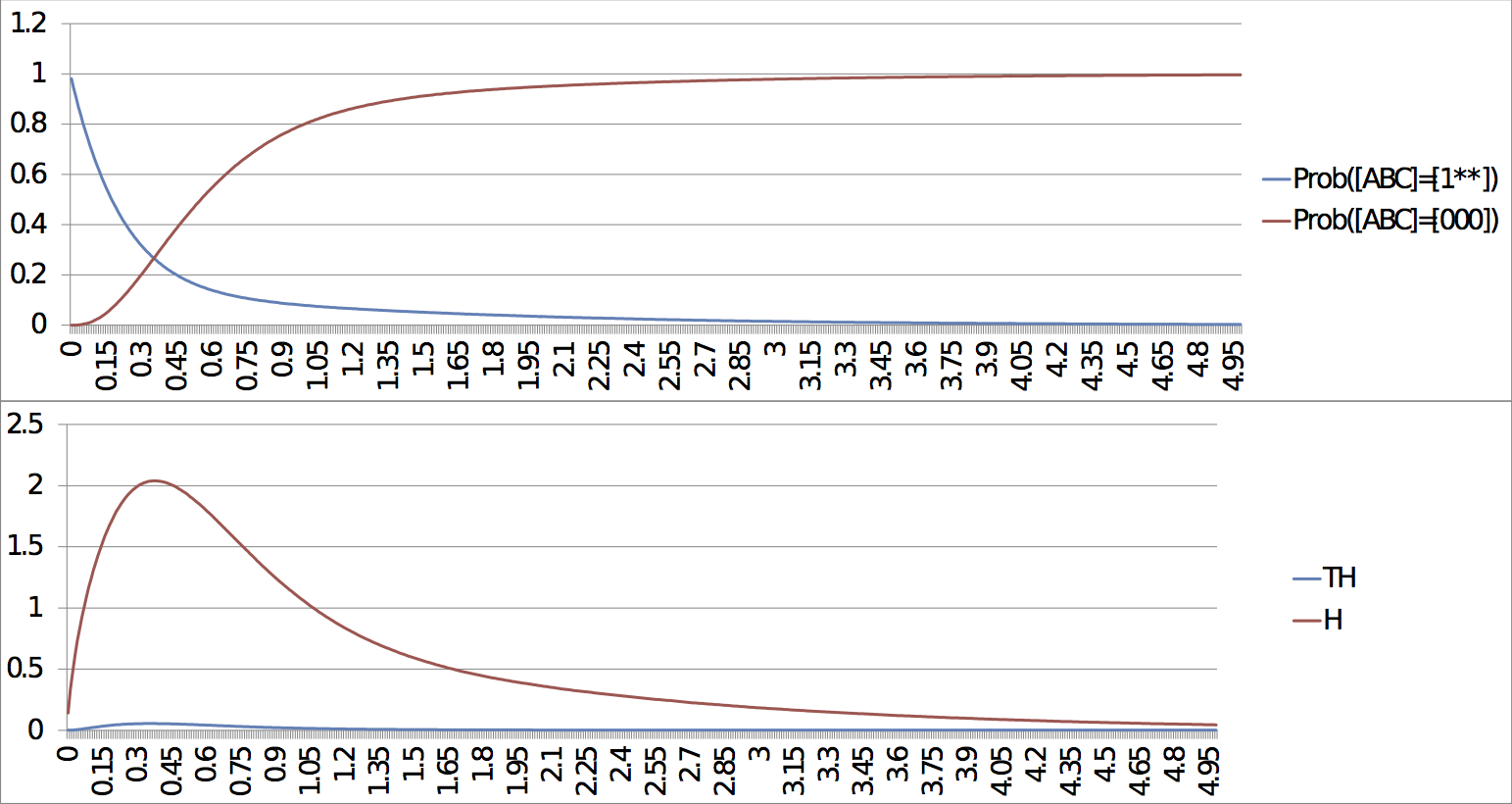
For the case of the slow escape, if we only look at early response, the probability simulations do not show the presence of the stable steady state but rather the system seems stuck in a limit cycle. It is only after a long time that the system reaches the stable steady state (entropy and transition entropy reach 0). The two simulations show both the transient and the asymptotic behaviours. Slow escape, early response: 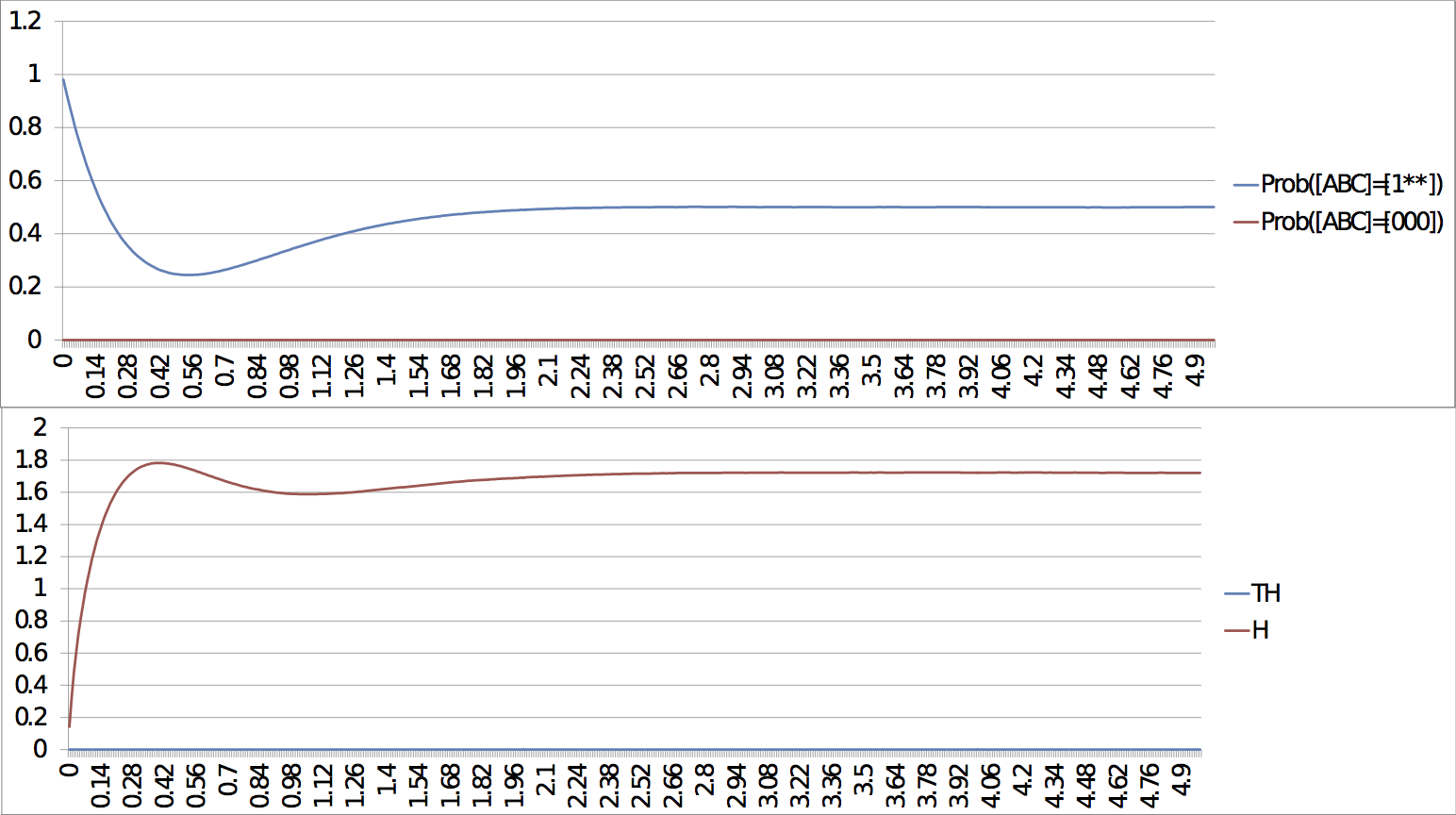
Slow escape, late response: 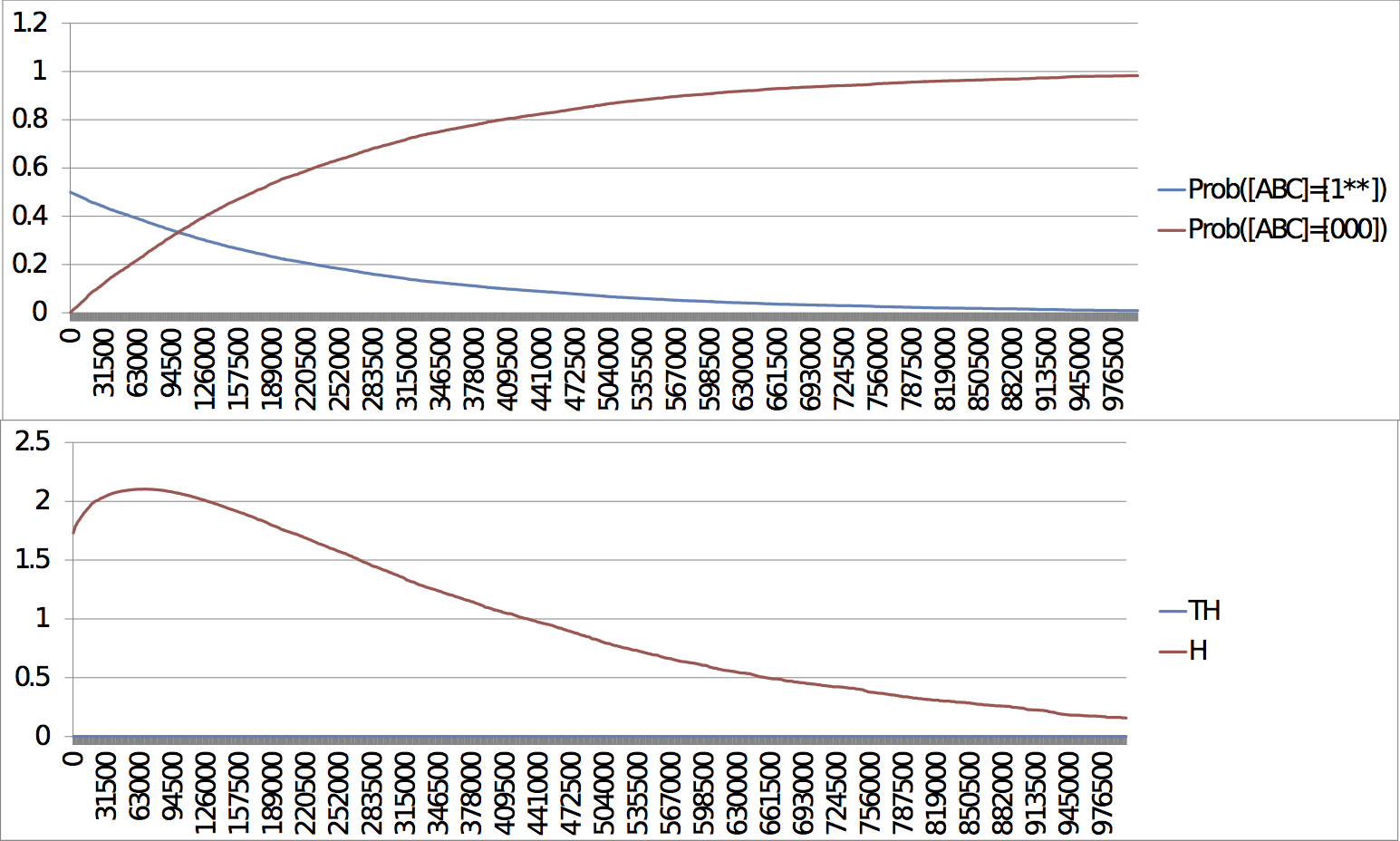
The output files can be found below: Cell CycleModel Description
The model is based on a published Boolean model of mammalian cell cycle (PMID:16873462), available on GINsim repository. It describes the signaling network that controls the mammalian cell cycle.
Influence Graph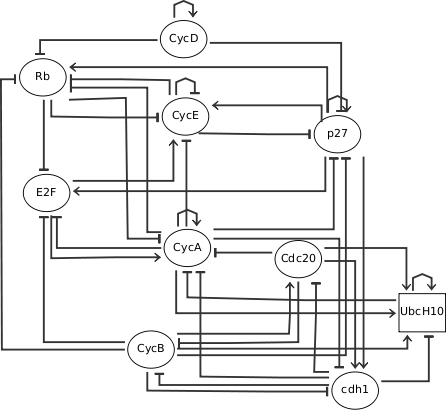
ModelThe model is described in the bnd file below. In the description of the model, we have included the possibility to simulate mutants. In the rate_down and rate_up terms, the parameters related to each mutant are referred to as $gene_del for deletion. They are set to 0 in the configuration file for the wild type and set to 1 when a mutant is modeled. The corresponding BND and configuration files can be found below:
Command lines: MaBoSS -c cellcycle_runcfg.cfg -o cellcycle_runcfg cellcycle.bnd MaBoSS -c cellcycle_runcfg_randinit.cfg -o cellcycle_runcfg_randinit cellcycle.bnd ResultsDamped oscillation can be observed on probablities of active cyclin. 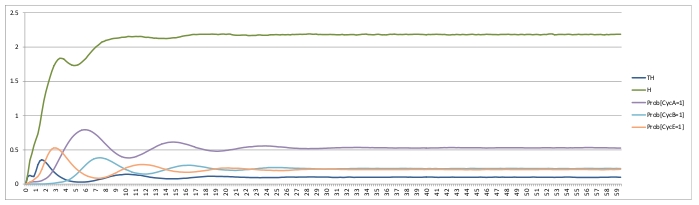
Modeling with a random inital condition produces two clusters, that represent two indecomposable stationary distributions 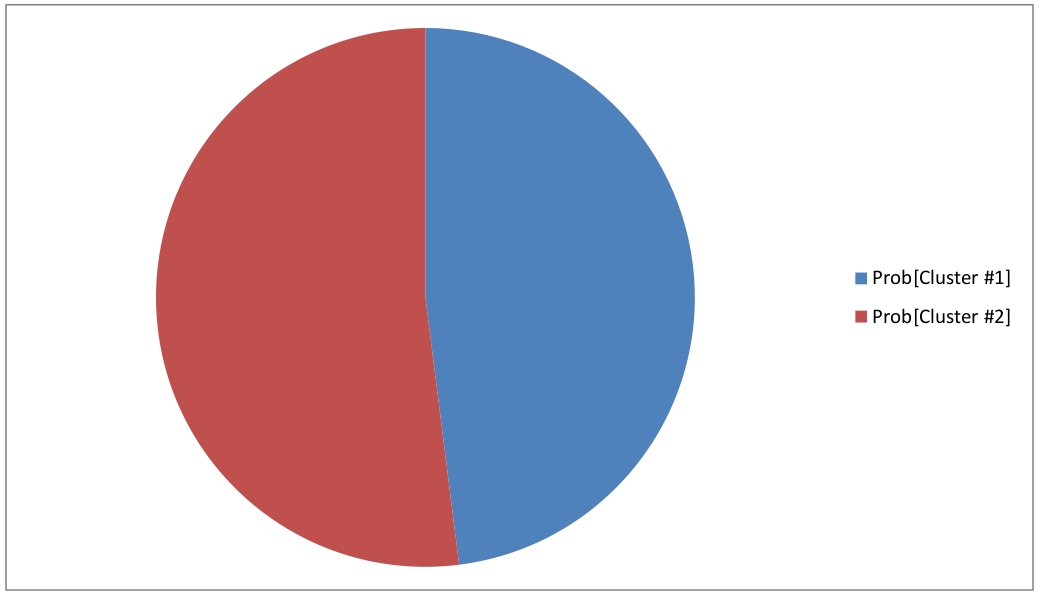
The first cluster can be interpreted in term of a disynchronized proliferating cell population 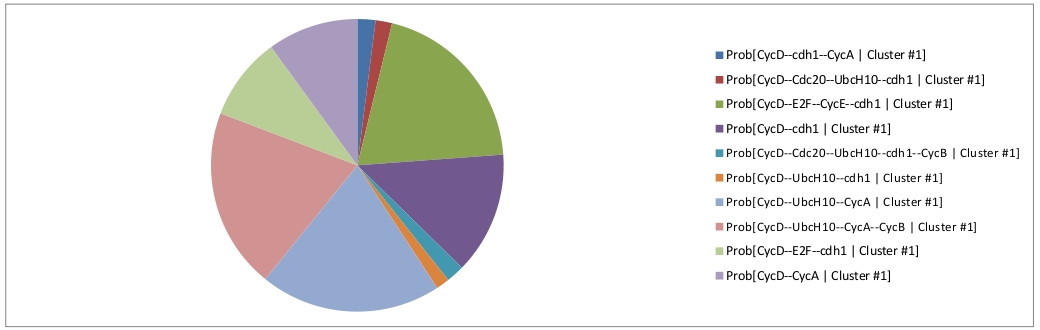
The second cluster can be interpreted as a fixed point, representing the G1 phase. 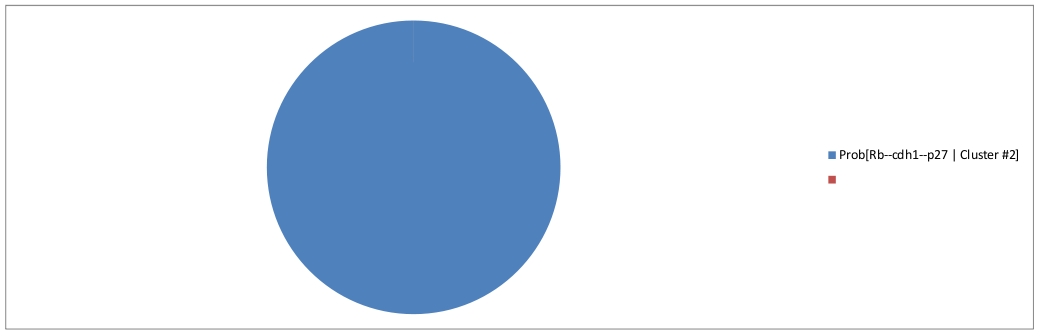
The corresponding output files can be found below: Cell FateModel Description
The cell fate decision example is based on a published Boolean model (PMID:20221256). It describes how the cell chooses between three different cell fates (apoptosis, NFkappaB activation and necroptosis) in response to cell death receptor engagement (through Fas and TNFR).
Influence Graph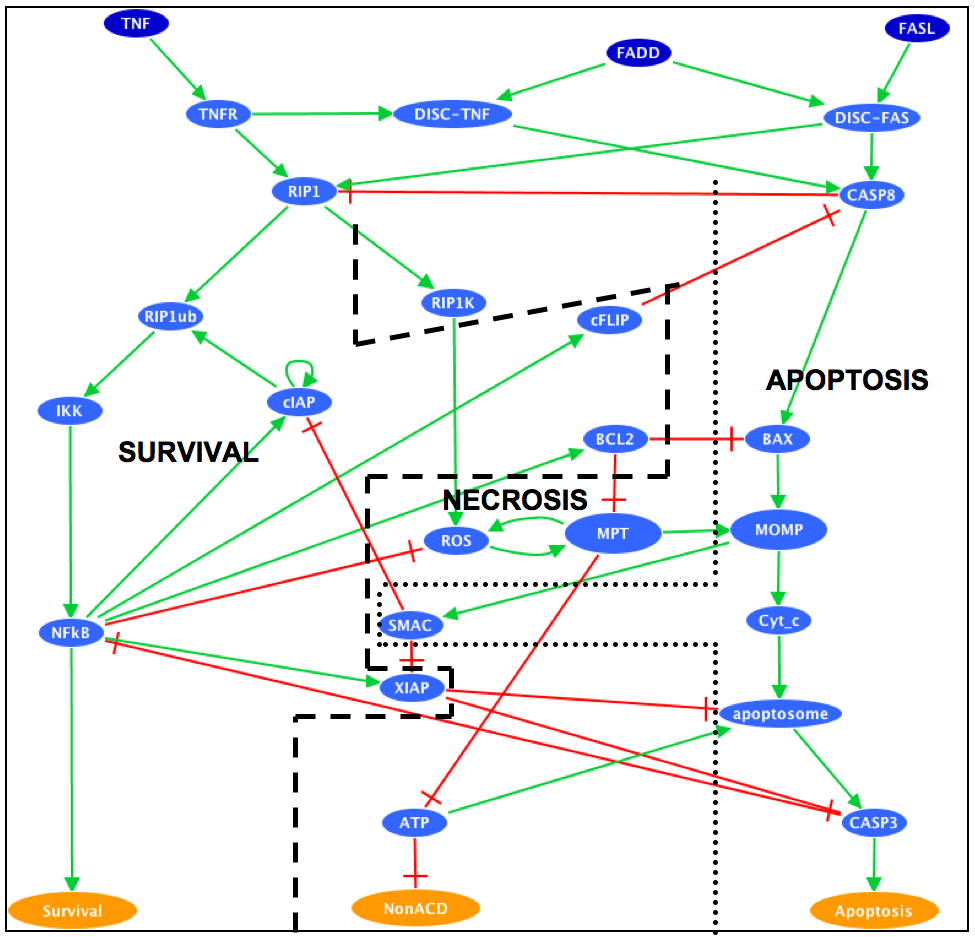
ModelThe model is described in the bnd file below. In the description of the model, we have included the possibility to simulate mutants. In the rate_down and rate_up terms, the parameters related to each mutant are referred to as $gene_del for deletion and $gene_oe for over-expression respectively. They multiply a constant (1000 here) and are set to 0 in the configuration file for the wild type and set to 1 when simulated. The corresponding BND and configuration files can be found below: Command line: MaBoSS -c CellFateModel.cfg -o CellFateOut_wt CellFateModel.bnd ResultsFor the wild type case, there are three stable steady states distributed as follows: 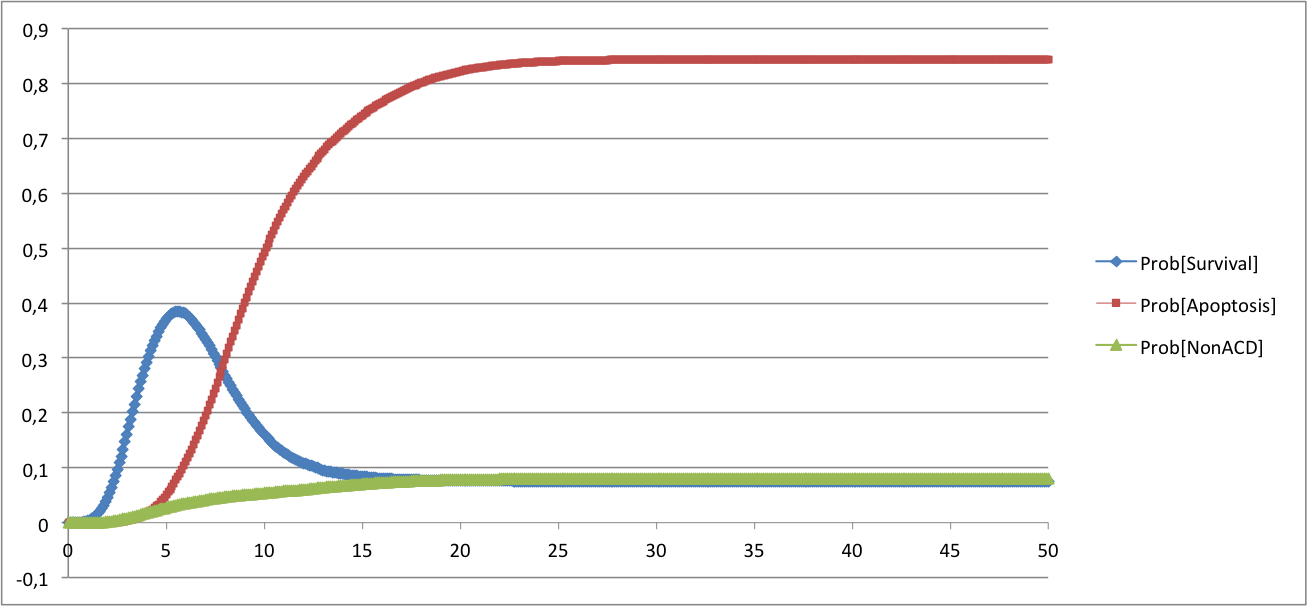
All the trajectories form three clusters that can be compared to the results of the published model. Qualitatively, the reachable phenotypes are the same. These probabilities are not absolute values as they depend on the computation and the details of the model itself. In the published model, the trajectories were computed over the transition graph. The published model showed the following phenotypes, where A stands for Apoptosis, N for Necrosis and S for survival: 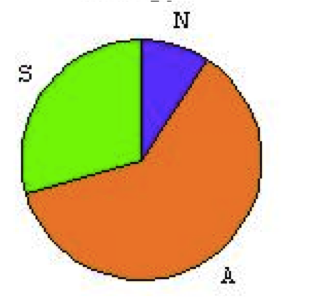
The model simulated in MaBoSS shows the same phenotypes with slightly different distributions: 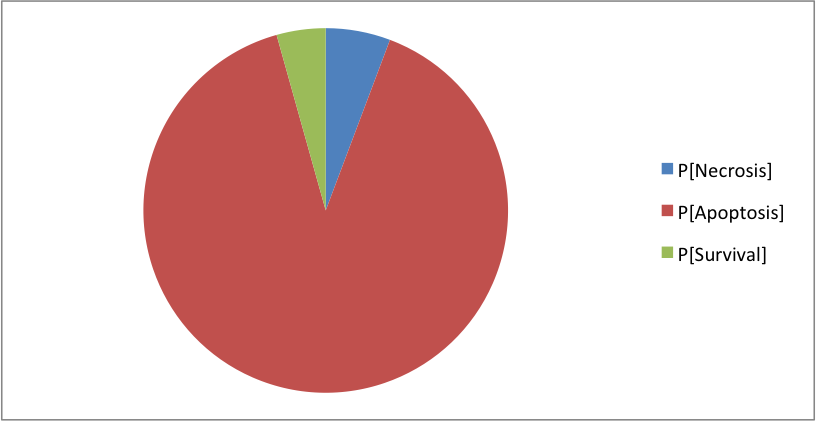
Where the clusters correspond to: [Apoptosis]=[TNF--TNFR--FADD--DISC_TNF--CASP8--CASP3--BAX--ATP--MOMP--SMAC--Cyt_c--apoptosome--Apoptosis] [Necrosis]=[TNF--TNFR--FADD--DISC_TNF--CASP8--BAX--MPT--ROS--MOMP--SMAC--Cyt_c--NonACD] [Survival]=[TNF--TNFR--FADD--DISC_TNF--RIP1--cIAP--RIP1ub--RIP1K--IKK--NFkB--cFLIP--ATP--XIAP--Survival] The simulation of CASP8 deletion shows the disappearance of one phenotype: apoptosis (in accordance with published experiments): 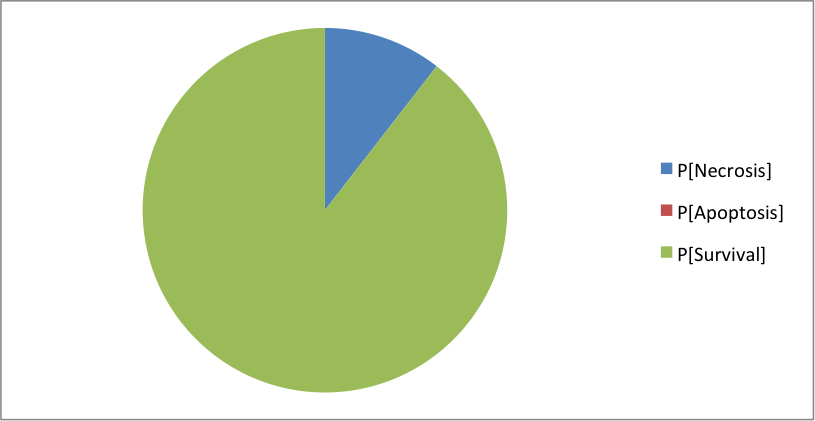
The corresponding output files can be found below: p53 / MDM2Model Description:We consider a published model of p53 response to DNA damage (PMID:19233211). p53 interacts with Mdm2, which appears in two forms, cytoplasmic and nuclear. On one hand, p53 upregulates the level of cytoplasmic Mdm2 which is then transported into the nucleus and inhibits the export of nuclear Mdm2. On the other hand, Mdm2 facilitates the degradation of p53 through ubiquitination. In the model, stress regulates the level of DNA damage, which in turn participates in the degradation process of Mdm2. p53 inhibits the DNA damage signal by promoting DNA repair. Influence Graph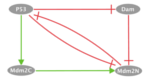
Transition GraphThe transition graph contains two cycles and a fixed point [p53 Mdm2C Mdm2N Dam] = [0010] where nuclear Mdm2 is on and the rest is off. 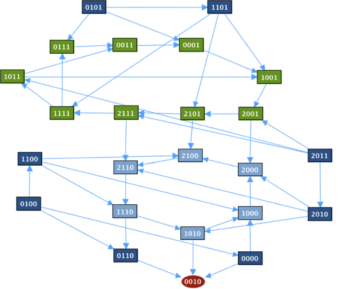
ModelBND and configuration files: Command line: MaBoSS -c p53_Mdm2_runcfg.cfg -o p53_Mdm2 p53_Mdm2.bnd ResultsThe trajectories of the probabilities of p53 being equal to 1 and p53 being equal to 2, with the initial condition: [p53 Mdm2C Mdm2N Dam] = [0*11] are plotted below: 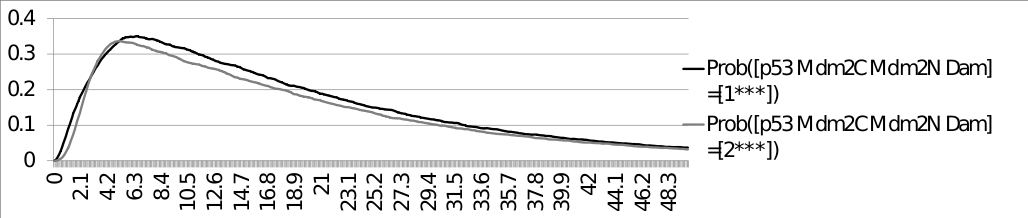
And the entropies: 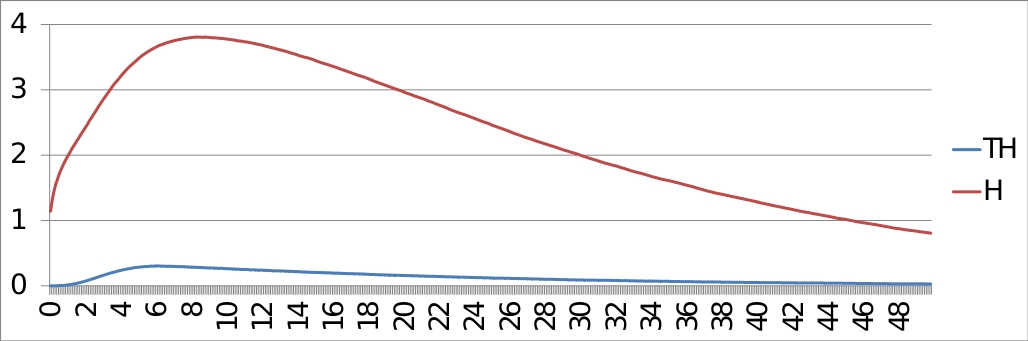
The corresponding output files can be found below: Drosophila PatterningModel Description
The model of segment polarity genes patterning is based on a published model (PMID:12782112). The following analysis is based on another publication (PMID:20655356); in particular, this publication studied the effect of random noise applied to the signaling network of segment polarity genes. The model consists of four identical signaling pathways, that are connected to each other. It represents the last step of drosophila patterning: the expression of the segment polarity genes. More precisely, this last step consists of a finer spatial patterning, driven by a set of genes (the segment polarity genes), whose expression last for a long time (compare to other genes involved in Drosophila segmentation).
Influence graph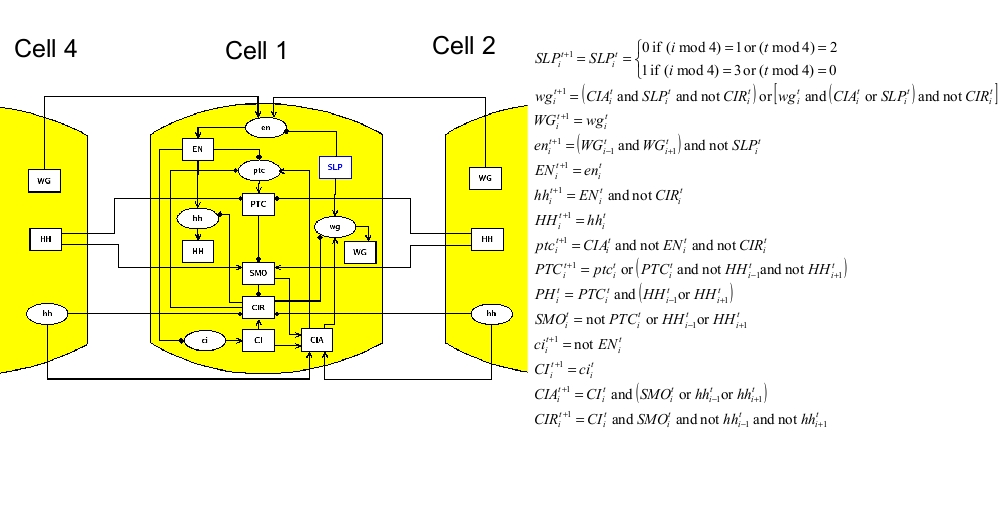
ModelLike in the two published papers, the model consists of four signaling pathways, one for each adjacent cell. mRNA and proteins are considered separately. Cell-cell interactions are represented by connections of one cell to the adjacent ones. For example, gene EN is transcriptionally activated by WG through the membrane; this is translated by including the following connections: WG4->en1, WG2->en1, WG1->en2, WG3->en2, WG2->en3, WG4->en3, WG3->en4, WG1->en4. The node en is written in lower case, because it represents the mRNA associated to the protein EN. Note that the model is "periodic", because cell 1 is adjacent to cell 4. SMO and PH are replaced by direct connections. The logical model is translated in MaboSS language. Two values of transition rates are considered: one for transcriptional influences ($rate_RNA=1), one for post-transcriptional influences ($rate_protein=10). The effect of random perturbation on every node has been included in the BND file; it can be tuned by the parameter $noise. The expected biological patterning is represented by the reference state below; none of the four cells are identical in term of node states. As described in the publications above, the model should produce the expected patterning, starting from a given initial state, when the pair rule gene SLP has the following pattern: SLP1,2=0 and SLP3,4=1. Two cases are considered: no noise ($noise=0) and low noise ($noise=0.01). 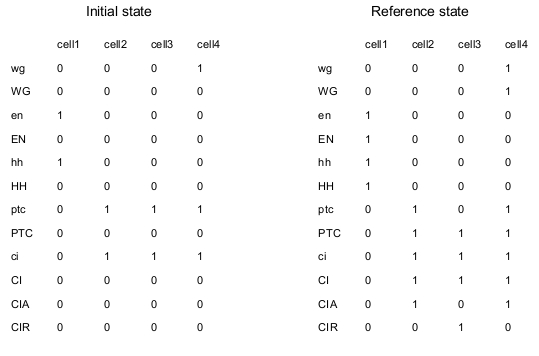
The corresponding BND and configuration files can be found below:
A specific configuration file for computing stationary distribution is provided for the following reason: it is easy to show that random noise on nodes expression ($noie>0) implies that there is only one indecompsable stationary distribution, with all network states with a non-zero probability (for the given intial condition). Therefore, the clustering algorithm for identifying indecomposable stationary distributions cannot give good results, seprating artificially stationary distribution estimates. In that case, it is more efficient to increase the maximum time, to lower the set of trajectories and to set the threshold for clustering to zero. Command lines: MaBoSS -c D_Pattern_ContT_noIntNode.cfg -o D_Pattern_ContT_noIntNode D_Pattern_ContT.bnd MaBoSS -c D_Pattern_ContT_noIntNode_noise.cfg -o D_Pattern_ContT_noIntNode_noise D_Pattern_ContT.bnd MaBoSS -c D_Pattern_ContT_noIntNode_noise_4statdist.cfg -o D_Pattern_ContT_noIntNode_noise_4statdist D_Pattern_ContT.bnd ResultsWhen there is no noise on nodes, the expected patterning is reached. This can be seen on the time trajectories of the Hamming distance distribution (with expected patterning as the reference state): 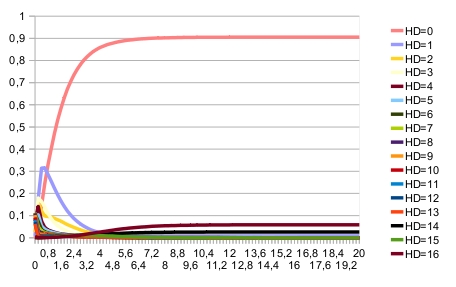
The asymptotic behavior consists of fixed points. Their respective probabilities are: 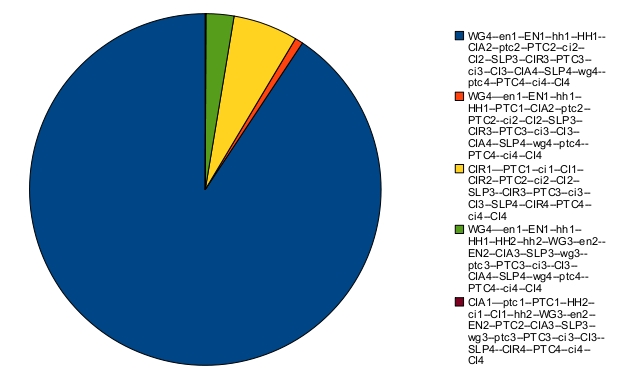
The blue fixed point corresponds to the correct patterning. When there is noise, the expected patterning is no longer stable. This can be seen on the time trajectories of the Hamming distance distribution (with expected patterning as the reference state): 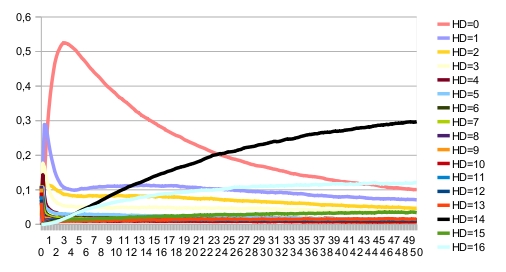
In that case, the asymptotic behavior consists of a single indecomposable stationary distribution: 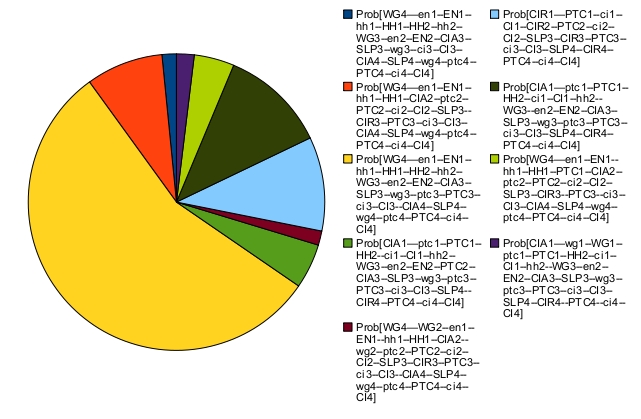
The most probable state (in yellow) corresponds to a "broad type" patterning (this state is defined in the publications above): two adjacent cells have identical node states. The corresponding output files can be found below: EGF-TNF SignalingModel Description
This model was used as an example for the standard language SBML qual and published in 2013 by Chaouiya et al.
The model can be found in BioModels database with the reference BIOMD0000000562.xls
Influence Graph
The model can be visualized with GINsim
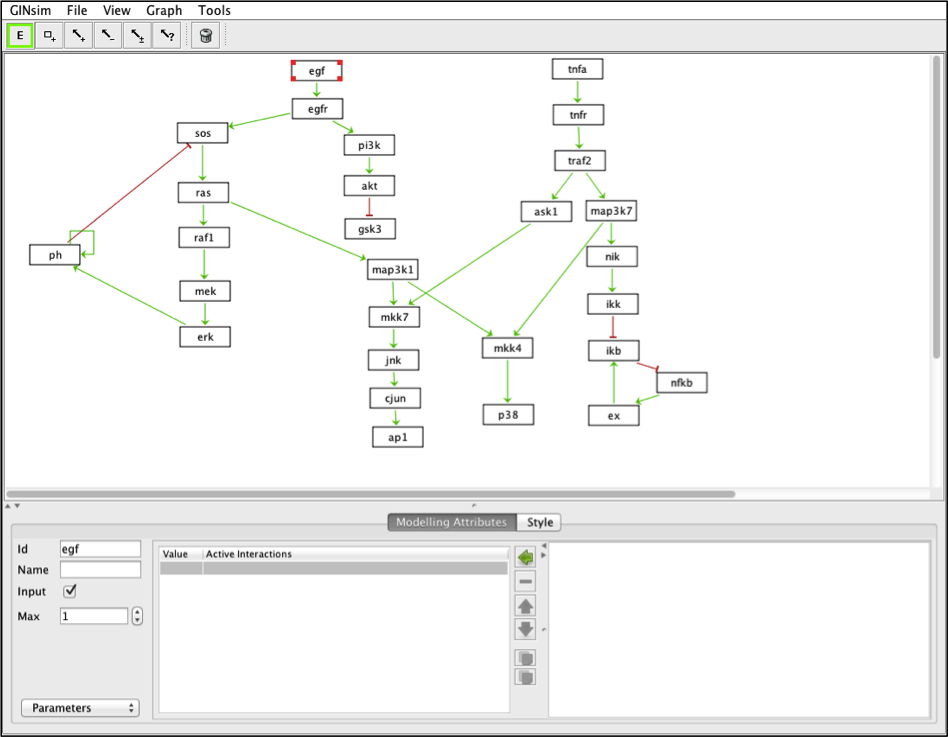 In GINsim, set egf and tnfa as inputs (tick the bow “Input” in the Modeling Attributes panel)
In GINsim, set egf and tnfa as inputs (tick the bow “Input” in the Modeling Attributes panel)
ModelThe bnd and the cfg files can be exported from GINsim. Chaouiya_maboss.bndChaouiya_maboss.bnd.cfg You can rename the cfg file into: chaouiya_maboss.cfg Some default parameters are applied during the export. The cfg file can be slightly modified by setting the appropriate initial conditions (by default all is at 0), and adding internal and external variables: erk.is_internal=1;ikk.is_internal=1; gsk3.is_internal=1; nfkb.is_internal=1; ask1.is_internal=1; ras.is_internal=0; egf.is_internal=0; egfr.is_internal=1; traf2.is_internal=1; ikb.is_internal=1; map3k1.is_internal=1; tnfr.is_internal=1; ap1.is_internal=1; mek.is_internal=1; mkk4.is_internal=1; ex.is_internal=1; tnfa.is_internal=1; raf1.is_internal=1; map3k7.is_internal=1; mkk7.is_internal=1; cjun.is_internal=1; sos.is_internal=1; jnk.is_internal=1; pi3k.is_internal=1; p38.is_internal=1; akt.is_internal=0; ph.is_internal=1; nik.is_internal=1; To visualize the fixed points: $ MBSS_FormatTable.pl chaouiya_maboss.bnd chaouiya_maboss.cfg 
And compare the results to the initial publications 
To visualize the outputs using a spreadsheet: as the plot of the sum of the three species ERK, AKT and RAS: 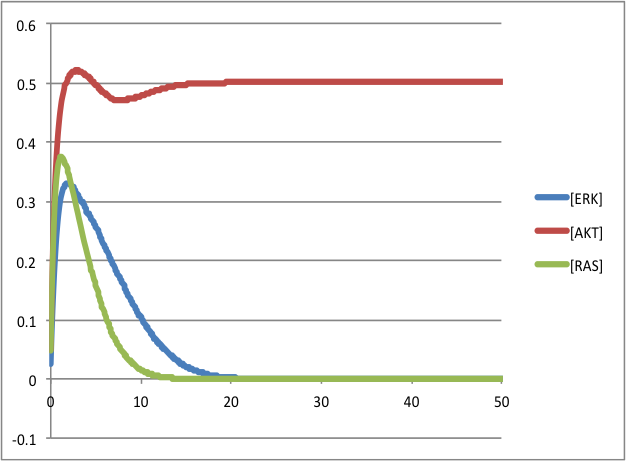
And compare it to the initial publication: 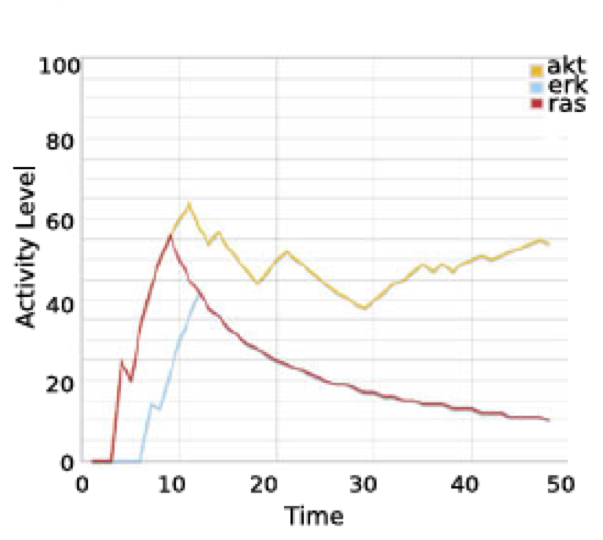
A tutorial is available here. Reference
Chaouiya C, Bérenguier D, Keating SM, Naldi A, Van Iersel MP, Rodriguez N, Dräger A, Büchel F, Cokelaer T, Kowal B, et al. SBML qualitative models: a model representation format and infrastructure to foster interactions between qualitative modelling formalisms and tools. BMC Syst Biol. 2013;7(1):135. doi: 10.1186/1752-0509-7-135.
Publications
Stoll G, Caron B, Viara E, Dugourd A, Zinovyev A, Naldi A, Kroemer G, Barillot E, Calzone L. MaBoSS 2.0: an environment for stochastic Boolean modeling. Bioinformatics btx123. 2017 Mar. DOI: https://doi.org/10.1093/bioinformatics/btx123 Documentation
MaBoSS: Reference Card for version 2.0
MaBoSS 2.0 tutorial is available, based on an example that illustrates all MaBoSS environment functionalites. For this tutorial, the following files are necessary:
Model in GINsim format Model in MaBoSS format: bnd file and cfg file Configuration file for MBSS_DrugSim.py Profile file for MBSS_MultipleSim.py File for MBSS_PrepareProjectFile.sh
SBML-Qual model tutorial: this tutorial provides an example of the use of MaBoSS with an SBML-Qual model downloaded from BioModels database.
Tutorials
> MaBoSS 2.0 tutorial is available, based on an example that illustrates all MaBoSS environment functionalites. For this tutorial, the following files are necessary: > SBML-Qual model tutorial: this tutorial provides an example of the use of MaBoSS with an SBML-Qual model downloaded from BioModels database. The Team
Contact
maboss.bkmc(at)gmail.com
|